Матричная лаборатория MatLab

 

Расчет триангуляции

В системе MATLAB определены функции триангуляции Делоне, триангуляции Делоне для ближайшей точки и поиска наилучшей триангуляции. Рассмотрим функции, реализующие триангуляцию Делоне.

  • TRI = delaunay(x.y) — возвращает матрицу размера mх3 множества треугольников (триангуляция Делоне), такую что ни одна из точек данных, содержащиеся в векторах х и у, не попадают внутрь окружностей, проходящих через вершины треугольников. Каждая строка матрицы TRI определяет один такой треугольник и состоит из индексов векторов х и у;
  • TRI = delaunay('x,у.'sorted'-) — при расчетах предполагается, что точки векторов х и у отсортированы сначала по у, затем по х и двойные точки уже устранены. Пример:
» rand('state',0);

» x=rand(1,25);

» y=rand(1,25); 

» TRI = delaunay(x,y);

» trimesh(TRI,x,y,zeros(size(x)))

» axis([0 1 0 1]); hold on;

» plot(x,y,'o')

  • dsearch(x.y ,TRI ,xi ,yi) — возвращает индекс точки из числа содержащихся в массивах х и у, ближайшей к точке с координатами (x1,y1), используя массив данных триангуляции TRI (триангуляция Делоне для ближайшей точки);
  • dsearch(x,y,TRI ,x1 ,y1 ,S) — делает то же, используя заранее вычисленную разреженную матрицу триангуляции S: S=sparse(TRI(: ,[1 1 2 2 3 3]), TRK: ,[2 3 1 3 1 2]).1.nxy.nxy), где nxy=prod(size(x));
  • tsearch(x,y.TRI,xi ,yi) — выполняет поиск наилучшей триангуляции, возвращает индексы строк матрицы триангуляции TRI для каждой точки с координатами (xi ,y1). Возвращает NaN для всех точек, находящихся вне выпуклой оболочки.
Триангуляция трехмерных и n-мерных массивов (п>=2) осуществляется при помощи функций delaunayS и delaunayn соответственно. Эти функции используют не алгоритм вычисления диаграмм Вороного, как del aunay, а алгоритм qhul 1 Национального научно-технического и исследовательского центра визуализации и вычисления геометрических структур США [ В MATLAB 6.1 функции delaunay, convhull, griddata, voronoi также используют qhull. - Примеч. ред. ].

Построенная по приведенному ранее примеру диаграмма представлена на рис. 17.1.

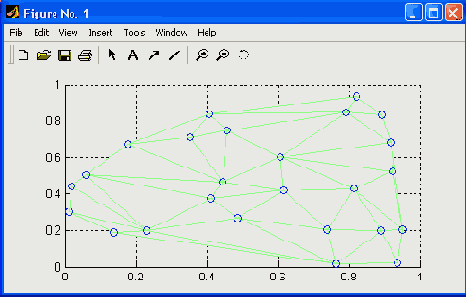
Рис. 17.1. Пример применения функции delaunay

 

Назад Начало Вперед