Матричная лаборатория MatLab
Вычисление полиномов
В этом разделе приведены функции вычисления коэффициентов характеристического полинома, значения полинома в точке и матричного полинома.- poly(A) — для квадратной матрицы А размера пхп возвращает вектор-строку размером n+1, элементы которой являются коэффициентами характеристического полинома det(A-sI), где I — единичная матрица, as — оператор Лапласа. Коэффициенты упорядочены по убыванию степеней. Если вектор состоит из п+1 компонентов, то ему соответствует полином вида c 1 s^n+...+c n s+c n+1 ;
- poly (г) — для вектора г возвращает вектор-строку р с элементами, представляющими собой коэффициенты полинома, корнями которого являются элементы вектора г. Функция roots(p) является обратной, ее результаты, умноженные на целое число, дают poly (r ).
1223 5
1112 32 » poly(A) ans = 1.0000 -58.0000 681.0000 818.0000 Приведенная ниже функция вычисляет корни (в том числе комплексные) для полинома вида
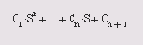
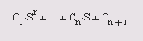
- roots (с) — возвращает вектор-столбец, чьи элементы являются корнями полинома с.
- polyval (p,x) — возвращает значения полинома р, вычисленные в точках, заданных в массиве х. Полином р — вектор, элементы которого являются коэффициентами полинома в порядке уменьшения степеней, х может быть матрицей или вектором. В любом случае функция polyval вычисляет значения полинома р для каждого элемента х;
- [у.delta] = polyval (p. x.S) или [у,delta] = polyval (p.x.S.mu)—использует структуру S, возвращенную функцией polyfit, и данные о среднем значении (mu(l)) и стандартном отклонении (mu(2)) генеральной совокупности для оценки пр-грешности аппроксимации (y+delta).
- polyvalm(p.X) — вычисляет значения полинома для матрицы. Это эквивалентно подстановке матрицы X в полином р. Полином р — вектор, чьи элементы являются коэффициентами полинома в порядке уменьшения степеней, а X — квадратная матрица.
|
»
D=pascal(5)
|
|||||
|
D
=
|
|
|
|
||
|
1
1
|
1
|
1
|
1
|
||
|
1
2
|
3
|
4
|
5
|
||
|
1
3
|
6
|
10
|
15
|
||
|
1
4
|
10
|
20
|
35
|
||
|
1
5
|
15
|
35
|
70
|
||